Bits og bytes

Det er lett å glemme at det er helt konkrete og fysiske prosesser som ligger bak alt som skjer i den digitale verden: Det hele er til syvende og sist bare elektriske signaler som flyr rundt i ledninger og kretskort, i fysiske maskiner av plast og metall.

Så hvordan fungerer egentlig disse maskinene? En PC består i hovedsak av prosessor og minne, i tillegg til inn- og utenheter som skjerm, mus og tastatur. Dette kalles maskinvare. I tillegg må vi gi presise og konkrete instruksjoner for hva maskinen skal gjøre til enhver tid. Dette kalles programvare.

Det som binder alt dette sammen er altså en uhyre stor mengde av elektriske signaler.

Det er disse signalene som er de berømte 0 og 1 – elektriske kretser, der det på et gitt tidspunkt enten er et signal (1), eller ikke (0). Når en utvikler skriver kode med instruksjoner til datamaskinen, vil dette under overflaten oversettes til maskinkode (0 og 1) som er det eneste maskinen egentlig kan forstå.

Et slikt signal er enkelt sagt det vi kaller en bit. Det er en forkortelse for «binary digit», altså et tall i binærsystemet, eller totallsystemet. En bit har altså kun to tilstander: av (0) eller på (1).

Dette systemet må vi bli litt bedre kjent med for å forstå hva digitale data i praksis er for noe og hvordan den digitale verden henger sammen.

Innsikt

Hvordan fungerer det binære systemet?

En enkelt bit gjør ikke så mye ut av seg, men i kombinasjon med andre bits er det dette som er grunnlaget for hele den digitale verden.

Nøkkelen til å forstå hvorfor dette er så genialt, er at vi kan bruke programvare til å få bits til å representere praktisk talt hva som helst. Og det skal ikke så mange bits til for å lage temmelig komplekse instruksjoner – på grunn av «magien» i eksponentielle tall.

Du har kanskje hørt historien om han som ba om et riskorn for første rute på et sjakkbrett, to riskorn for andre rute, fire for tredje, åtte for fjerde – og så videre? Altså en dobling for hver av de 64 rutene på brettet. Det høres ut som en nokså ydmyk forespørsel … inntil du begynner å gjøre matten: Innen du kommer til siste rute, vil det være snakk om 18.446.744.073.709.551.615 riskorn!

Det er akkurat det samme prinsippet som gjør kombinasjonene av 0 og 1 så smart: For hver bit du legger til, vil du doble det totale antallet mulige kombinasjoner du har å jobbe med. Med én bit har du bare 2 mulige tilstander, men med to bits har du 4, tre bits gir 8, fire bits gir 16, fem bits gir 32 … og før du vet ordet av det, er du oppe i millioner og milliarder.

Og disse kombinasjonene kan altså programmeres til å representere hva som helst.

En serie signaler, som 01101101, kan for eksempel fortelle maskinen at den skal gi deg bokstaven «m» når du jobber i et tekstbehandlingsprogram. Mens nøyaktig de samme åtte bitene kan representere en nyanse av rød, grønn eller blå (RGB) i en piksel i en digital bildefil. Slik jobber maskinvare (selve maskinene og de elektriske signalene) og programvare (instruksjonene og reglene for hva disse signalene skal representere) sammen for å skape hele den digitale virkeligheten.

Lær å telle binært

La oss stoppe opp litt og forstå enda litt bedre hvordan det binære systemet faktisk fungerer.

Tenk at du har en eske med Lego, og lurer på hvor mange klosser det er i den. Du har ikke noe å skrive på, og begynner å telle på fingrene … men kommer da åpenbart bare til ti. Det blir litt for lite! Men med binære tall, derimot, kommer du helt til 1023 (eller 1024 hvis du regner med 0).

Som du nå har skjønt: Det som gjelder er ikke antall fingre du har å telle på, men antallet mulige kombinasjoner av de ti fingrene.

Antall mulige kombinasjoner kan vi enkelt regne ut med enkel potensregning, med 2 som grunntall og antall bits som eksponent. Antallet mulige kombinasjoner med ti fingre er da to opphøyd i ti, altså 2^10 = 1024.

Hva om vi tar med tærne også, og altså totalt jobber med 20 bits? Da blir det kanskje noen tusen til? Vel, det er lett å sjekke: To opphøyd i tjue er … 1.048.576!

Prøv det selv – tell til 1024 på fingrene!

Vil du se hvordan det fungerer? Dette er egentlig ganske enkelt – og gøy – så snart du skjønner logikken. Det er også et bra partytriks hvis vennene dine er like kule og nerdete som deg.

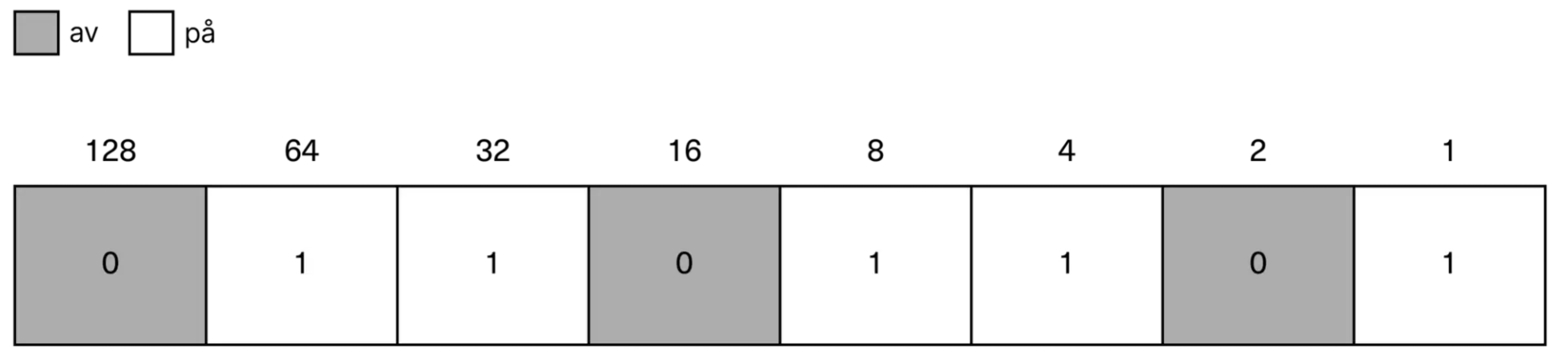
Bytes: Kombinasjoner av bits

Akkurat som at bokstaver må bli til ord for å brukes til å formidle noe, lager vi kombinasjoner av bits for å utrette noe på en datamaskin. Kombinasjonen av åtte bits er det som kalles en byte. En byte kan representere 256 ulike verdier (2^8 = 256).

Hver bokstav og hvert tall du ser på skjermen foran deg vil være representert med én byte i datamaskinens grunnleggende kode. Bits og bytes kan representere hva som helst, ikke bare tall, men også bokstaver, farger, lyd, kundedata, fotballresultater eller hva som helst annet.

1000 (noen vil si 1024) byte er en kilobyte, 1000 kilobyte er en megabyte, 1000 megabyte er en gigabyte, og så videre. Det er over en milliard bytes i en gigabyte, og dermed over åtte milliarder bits. Hvis vi da tenker på antall mulige kombinasjoner og sammensetninger, får vi et større tall enn vi har plass til å skrive her.

Alt du har på maskinen din – bilder, programmer, tekstdokumenter – er lagret og blir behandlet på denne måten, som sammensetninger av bits og bytes. Det er slike sammensetninger vi bruker for å representere ulike ting i data.

Slik jobber maskinen med bits og bytes

Det er datamaskinens programvare som forteller maskinvaren hva den skal gjøre med de elektriske signalene den mottar (altså bits) i ulike sammenhenger.

Jobber du for eksempel i et tekstbehandlingsprogram og trykker på bokstaven «m» på tastaturet, mottar maskinen som tidligere nevnt signalene 01101101. Dette er, som du nå ser, én byte – åtte bits. Programvaren forteller maskinen at når den får akkurat disse signalene, skal den lage en «m» i tekstdokumentet ditt.

Hvis du nå telte deg frem til at 01101101 tilsvarer tallet 109, etter systemet du lærte da du telte på fingrene, blir du sikkert glad for å høre at den såkalte ASCII-koden for en liten «m» er nettopp 109.

ASCII-tegnsettet (kort for American Standard Code for Information Interchange) er en standard for hvordan tall, bokstaver og annen input fra tastaturet skal representeres som digitale data. Standarden ble innført allerede i 1963, og er fortsatt i bruk som del av den nyere standarden UTF-8 (Unicode Transformation Format 8, altså en variant av Unicode-tegnsettet).