Sannsynlighet
Statistikk brukes ofte som beslutningsgrunnlag i moderne bedrifter, organisasjoner og myndighetsorganer. Nøyaktig hva som er best eller mest fordelaktig å gjøre i en gitt situasjon er som regel vanskelig å vite. Men gjennom god bruk av data og statistikk kan vi i mange tilfeller likevel ta beslutninger basert på hva som mest sannsynlig gir et ønsket resultat.
Sannsynlighet var lenge en nokså uhåndgripelig størrelse. Opp gjennom historien har oppfattelsen av tro, skjebne og flaks ofte tatt plassen sannsynlighet har i dag.
På mange måter kan vi takke gamblere og hasardspillere fra 1600-tallet for at sannsynlighetsregning ble tatt på alvor. Dette er aktiviteter der det er store gevinster, og veien til disse gevinstene er brolagt med flaks og – nettopp – sannsynlighetsberegninger.
Det var i jakten på slike gevinster at tre franskmenn rundt midten av 1600-tallet henvendte seg til den kjente, franske matematikeren Blaise Pascal. På denne tiden var det en etablert «sannhet» at man i et terningspill med to terninger og 24 kast nokså sikkert kunne vedde på at man på ett eller annet tidspunkt ville kaste doble seksere. Men i Pascals utregninger så man at dette slett ikke var et sannsynlig utfall; snarere tvert imot.
I tillegg til dette noe enklere spørsmålet stilte franskmennene også et spørsmål om hvordan potten skulle fordeles på rettferdig vis, dersom man stanset spillet før det var ferdigspilt. For dersom man på forhånd hadde bestemt at vinneren ville innkassere hele potten, så hadde man jo i praksis ingen regel for hvordan potten skulle fordeles kun ut ifra hvor sannsynlig det var at hver spiller ville ha vunnet.
Dette problemet løste Pascal i en brevveksling med en annen matematiker, og la dermed grunnlaget for moderne sannsynlighetsteori. Løsningen? Det vi i dag kjenner som forventningsverdi. Verdien er ikke identisk med et faktisk utfall, men den tilnærmer seg gjennomsnittet av de faktiske utfallene dersom man hadde utspilt hendelsene.
Sannsynlighet lar oss håndtere usikkerhet
I dag bruker vi datamaskiner til å beregne sannsynlighet og simulere utfall i ulike situasjoner. I et dataprogram kan man gjennomføre millioner av simuleringer av terningkastene i Pascals problem på et øyeblikk, og dermed få et godt beslutningsgrunnlag raskt og enkelt.
Det betyr at vi kan bruke sannsynlighetsregning til å hjelpe oss med mye mer sammensatte utregninger enn det som var mulig på Pascals tid.
Eksempel
Terningkast
Det er mange måter å illustrere sannsynlighet på, men terningkastene er et enkelt og forståelig eksempel I illustrasjonen under kan du se resultatet av at vi kjørte 10.000 simuleringer av to terningkast i et åpent tilgjengelig verktøy (GeoGebra). Summen av øynene på to terninger kan være fra 2 til 12 på et kast. Diagrammet viser hvordan summen av terningene fordelte seg på 10.000 kast.
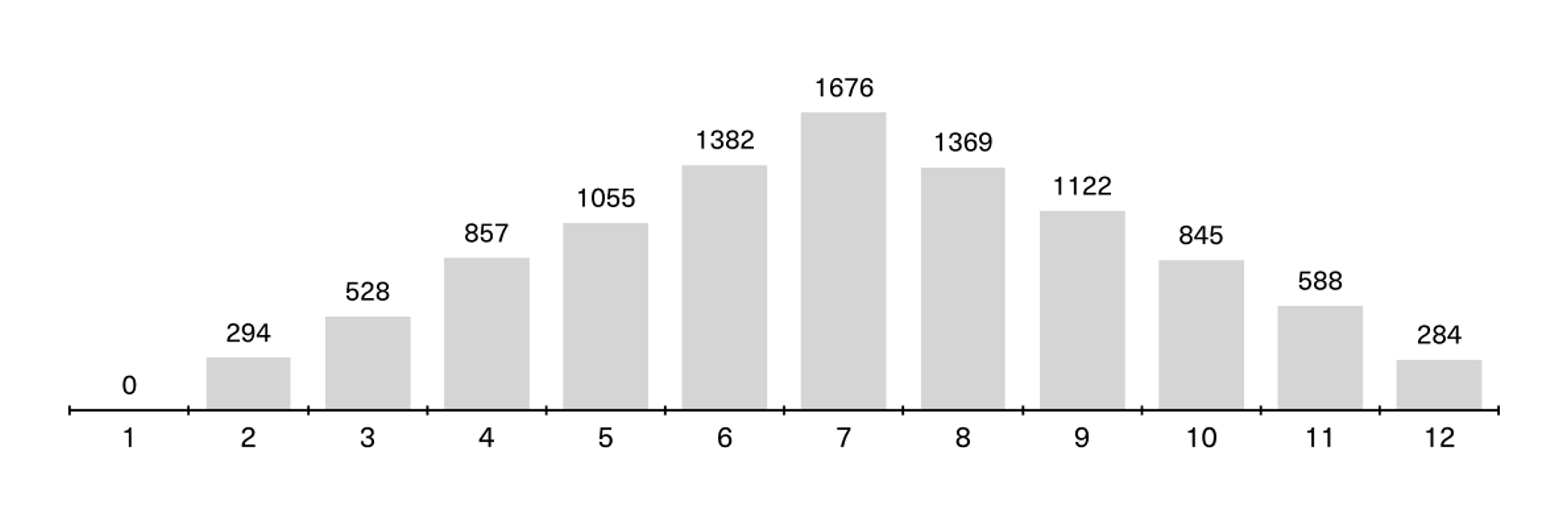
Om vi går tilbake til eksempelet med doble seksere fra Pascals eksempel, kan vi se at av 10.000 kast var kun 284 tilfeller der doble seksere ble utfallet. (Her ser du forresten et godt eksempel på en normalfordeling!).
Eller med andre ord: det er omtrent 2,8 prosent sjanse for å trille doble seksere i et slikt spill. Den sannsynligheten viser til et enkelt kast, ikke på tvers av de 24 kastene som utgjør et spill, som nevnt tidligere.
Dette gjelder selvsagt også alle andre varianter av doble tall. Hvis du legger til enda en terning faller sjansen til omtrent 0,5 prosent. Men dersom du vedder på at summen av to terninger vil ende opp med verdien 7, vil du ha relativt gode odds; hele 16,7 prosent! Det er fordi du kan få dette resultatet på flere måter, enten du kaster 1+6, 2+5 eller 3+4.
Dersom du var franskmann, spillegal og ville ha mest mulig gevinst for pengene dine, var det altså høyt spill å satse alt på doble seksere.
Dette illustrerer grunnen til at mange i dag understreker sprengkraften i digitale verktøy, og de enorme kreftene vi i dag håndterer når vi jobber datadrevet. Der vi har tilgang på tilstrekkelig med data i god kvalitet kan vi med hjelp av sannsynlighetsregning simulere hvordan ulike situasjoner og prosesser vil utspille seg, og i neste omgang bruke dette til å ta bedre beslutninger. Det er en viktig grunn til at data kan være så verdifullt for bedrifter, organisasjoner og myndighetsorganer.
Som du ser, handler dette langt på vei om å håndtere usikkerhet. Hvor mange biler vil bilselgeren selge i morgen? To, femten, null eller tre hundre?
Vi trenger ikke gjette, men kan bruke data og utregninger for å komme frem til et godt svar. Hvor mange biler hun solgte i går, forrige måned og på denne tiden i fjor tar oss et godt stykke på vei. Så kan du begynne å se etter andre faktorer som kan spille inn: kanskje får bilselgeren hjelp av solskinnsvær, reklamekampanjer, en opptur i økonomien og en premiere på en blockbuster-bilfilm.
Her må du se etter og vurdere korrelasjoner og årsakssammenhenger, og ganske snart er du i ferd med å stable sammen et intrikat regnestykke – som til slutt kan gi et mer eller mindre presist estimat for sannsynlige salg. Eller sagt med et annet ord: en simulering.
Til slike utregninger og simuleringer brukes i dag ofte maskinlæring. Ved hjelp av maskinlæring kan vi kartlegge mønstre i store datamengder som det typisk ville vært helt usannsynlig for oss mennesker å identifisere på egenhånd – slik som hvilke faktorer som reelt sett spiller inn på salget av biler. Kanskje viser det seg å være helt andre ting enn det du intuitivt så for deg. Men i dataene finnes svar.
Slik kan datadrevet arbeid avdekke og belyse sannheter som ellers ville forblitt tilslørt for oss mennesker, og gi oss handlekraft og beslutningsgrunnlag for å ta bedre avgjørelser og påvirke utfallet av arbeidet vårt i en mer ønskelig retning.
Vår verden sett gjennom usikkerhetens og sannsynlighetens linse
Statistisk inferens
Som nevnt er sannsynlighetsteori først og fremst egnet for å redusere usikkerhet, ikke for å eliminere den fullstendig. Selv med kraftige datamaskiner og millioner av simuleringer vil sannsynlighetsteori (sannsynligvis) aldri bli en eksakt vitenskap.
Dette er egentlig ganske selvsagt; det er sjelden vi kan være helt sikre på noe som helst. Men om hundre prosent garantert sikre prediksjoner eller funn skulle vært en forutsetning for vitenskapelige fremskritt, ville vi levd i et ganske annerledes samfunn enn vi gjør i dag. De fleste prosesser ville nok stoppet opp før de engang startet, om man ikke aksepterte en viss grad av usikkerhet.
Vi vil dessuten som regel aldri ha tilgang på absolutt alle relevante data om en ting. Når vi skal undersøke noe som er stort og uoversiktlig, trekker vi derfor ofte ut begrensede utvalg av større populasjoner – et såkalt «representativt utvalg». Dette er et verktøy som ofte brukes i forbindelse med spørreundersøkelser, og en lignende teknikk benyttes ofte i møte med andre typer datakilder.
Det vi snakker om her er såkalt statistisk inferens, der man trekker konklusjoner om en større gruppe basert på det tidligere nevnte begrensede utvalget. En slik gruppe omtales gjerne som en «populasjon», men ikke slik begrepet brukes på engelsk; her menes det kun en spesifikk mengde individer eller objekter med noen felles egenskaper.
«Inferens» kan enkelt oversettes til en utledning, altså en konklusjon man gjør seg opp ved hjelp av logiske slutninger basert på informasjonen man har. Statistisk inferens er altså en mer skjønnsmessig vurdering av sannsynligheten for at noe er sant i en større populasjon, heller enn en simulert beregning.
Dette brukes ofte i vurderingen av legemidler, for eksempel. Når en ny vaksine rulles ut i en befolkning, er det vanskelig å si hvor effektiv den er på befolkningen som helhet. Derfor gjør man et representativt utvalg av befolkningen, og skalerer opp funnene fra dette utvalget til resten av populasjonen. Da kan man si noe om vaksinens effekt og eksempelvis sannsynliggjøre hvor store kostnader sykdommen (som vaksinen skal beskytte mot) vil medføre, eller hvor sannsynlig det er at noen vil bli alvorlig syke av å bli smittet etter å ha blitt vaksinert.
Statistisk inferens kan gjøres ved hjelp av mange ulike metoder. I neste emne, som handler om maskinlæring, skal vi gå nærmere inn på én av dem: regresjonsanalyse.